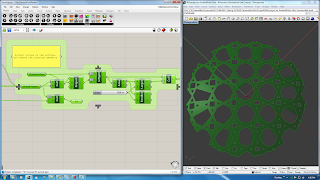
Project 2

Project 1 update...

project 1 updated method  I:

Because there were some inconsistency in the results for project 1 , I have decided to revise the method. In project one there were inconsistencies with the sizes of the panels. The panels that were in the middle of the dome had no distortions, however, the panels that were closer to the edge were distorted. In order to solve the problem I have revised the way in which the dome surface is generated. 

After extracting the mesh from the Kangaroo engine, I extracted only one curve from each mesh, which is the curve that has the longest span. This curve was then duplicated/offset in both directions. The distance that the curve is moved by was extracted from the original mesh by calculating the area of the original mesh and getting its square root. Thus the curves will always offset parametrically to the size of the mesh, eliminating the possibilities of error. 

In this step the three generated curves are lofted to create the base surface for the dome.

Here the surface is divided equally in the both UV directions.

Then the center of each panel is extracted 

If we are to imagine the dome being part of a great sphere, we connect the center of the sphere to the new points generated in the center of each division created in the last step to find the normal at that point. Of course there are other methods to find the normal, but I have found this method to have better accuracy when it comes to plane rotation. 

The new generated planes

Here, the original curve for a single panel is oriented to the newly created planes on the surface. 

Offset the pattern in the positive and negative direction to generate the basic curves for the panels.

Create a planar surface from each series of planar curves, and extrude them based on their normal.

Generate a Box with a Z parameter that stops at the bottom of the desired dome result. This Z value can also be extracted from the original mesh.

The panels and the Box are then differenced to create the final resulting panels for the dome.

project 1 updated method  II:

The second method is a combined method of what was done in Project 1, and project 1 updated method I. Basically after extracting the mesh from the Kangaroo engine, we go through the same steps to generate the basic surface of the dome.

The dome out of the Kangaroo engine

Exploding the dome to its elements

Creating a curve that spans the length of the dome.

Parametrically offsetting the curves.

Lofting the curves to create the basic shape for the dome. 

Subdividing the dome to prep it for the BoxSurface.

Applying the BBox method as in Project 1 to the BoxSurface.

Generating a parametric box which will then be used for a difference/Boolean operation.

Final outcome of a single layer in the dome.

Final outcome for all Four layers of the dome.

Final outcome of the dome and the project masses. 

Project 2 methods:

The basic idea for project 2 is to affect the panels that are applied to the dome. The idea is to create panels that are responsive to the sun. In order to do this, the normal vector of each panel needs to be generated and then compared with the angle of the sun. Where the angle between the normal vector and the sun vector is 90 degrees, the panels elements will become thicker to prevent the sun from penetrating the space. In contrast, where the larger/smaller the angle is from 90 degrees, the panels become thinner because there is no need to provide shading as the sun will be automatically blocked. Because each panel will be affected differently, the BBox method used in Project 1 will not work. 

Three different methods were used to create the desired affect. All three methods use projection to generate the pattern on the dome surface.

Project 2 method I : By distance from the flat pattern

This is the simplest and most straight forward method. The basic idea is that we can conceptually consider the sun at a very close proximity to the building.  By doing so, we can compare the distance between the sun and each panel/curve .

First we generate the flat pattern. note that the pattern in the image is affected by the sun.

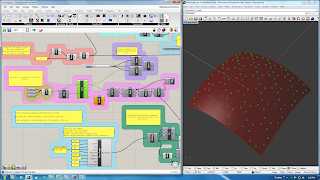
Then we create the sun and decide for which time of the year we are conducting the experiment. To do that, I have utilized a very nice Sun Vector node that can be found in this Sun Vector Link . The Sun Vector node allows for different parameters to be controlled which can simulate the location of the building and the different sun vectors throughout the year.

The series of nodes shown in the image are created to generate different points and planes for the pattern so that the number of panels on the dome can be parametrically controlled.

These nodes control the scale of the pattern on the dome which is also parametric.

Here we calculate the distance between each panel and the sun.

The distance is processed and then is passed to the offset parameters for the flat curves.

The flat curves are then projected on the dome.

Originally, I wanted to use Galapagos to analyze each step throughout the year in order to come up with the most efficient design for the patterns. However, because the projection process on the dome is processor and memory intensive, that idea was left for future exploration. Nevertheless, in order to prepare for that step, there are two options to generate the dome, one which uses poly Surface, the other uses a Mesh which is what is required by analysis/visualization plug-ins.

Project 2 method II : By distance from the Dome

Here we measure the distance between the conceptual sun and the dome. To do that, a series of points were generated from the flat pattern and are projected on the dome. It is important to generate these points from the pattern itself as each point will correspond to the curve that it was generated from, thus the distance to the point will affect the curve. 

 These points are evaluated for there normal direction which will be used in the last method.

With this series of nodes we measure the distance between the sun and the points

The distance is then processed and passed to the curves which are offset based on the processed distance.

Finally we project the curves on the dome to generate the pattern.

Project 2 method II : By angle between the sun and the Dome

The same steps were followed as in the previous methods. However, now instead of the distance we measure the angle between the sun vector and the surface vectors. A VB node was used to reset the angle when the angle exceeds 90 degree.

ARCH689 Project 1

The Louvre, Abu Dhabi

by Jean Nouvel

status: under-construction

“A large, shallow dome, 180m in diameter, floats above the collection of buildings, with only four support points around its perimeter truss. The dome unites this micro-city, and takes up the Islamic tradition of the perforated screen and the use of self- similarity and fractal organization of patterning to create a special micro-climate below. The space beneath is animated by the shadow play caused by the modulation of light by the complex, lacy mesh of small openings across the dome’s surface, reflected on the buildings and the water of the inlet.”

Study of the initial duplication of the fractal pattern

Study of the initial duplication and 12.5 degrees step rotations of the fractal pattern

Result of the initial duplication and rotation of the fractal pattern

Fractal pattern studies

Fractal pattern shadow studies:

This experiment was done using a software called modo. The pattern in this rendering is procedural, not generated from the previous diagrams.

This experiment was done using a software called modo. The pattern in this case is a direct translation of the diagrams into a three-dimensional surface.

The Louvre in Grasshopper

Step1: building outlines in Rhino:

The first step was to create the outline of the building in Rhino which is then used in grasshopper to generate the massing. Because of the minimal infor- mation published about the project, not all the masses match the heights in the original design by Jean Nouvel. However, a study of the shadow casting from one of the published renderings provided the proportional relationship between the different heights of the masses. In the image below, each color represents a group of masses that share the same height parameter.

Step2: from Rhino outlines to Grasshopper masses.

The outlines from the previous step were transferred to Grasshopper where every group’s height is controlled by a slider.

Step3: volumes global parameter

The height of the whole building and all its masses is controlled by a multi- plier. This multiplier allows for the change of all the volumes in the design proportionally. This in return will maintain the relationships between all the volumes.

Step4: mass local parameters

While there is a multiplier to control the relationship between the masses, each group of volumes have the ability to change its height parameter lo- cally, which will allow for a greater set of variations.

Step5: dome as flat mesh

In this step the process of creating the dome starts. It will become evident in the following steps why a mesh was used instead of a surface. There are four meshes in total where each layer will be used to create on of the outer layers of the dome.

Step6: from a flat mesh to a dome via Kangaroo

The four meshes created in Rhino in the previous step will be fed to a Kangaroo definition within the over-all definition for the building. By giving Kangaroo a U-Force node in the positive Z direction, the flat mesh takes the shame of a dome.

Step7: extracting meshes

In this step, we take the four different meshes that were fed into Kangaroo and separate them.

Step8: extracting curves from meshes

Here we create a series of curves that define the mesh.

Step9: lofting and subdividing

In #1 we loft the curves created in the previous step to create a surface type object for the dome.

#2 shows the number of subdivisions on the surface which can be increased or decreased parametrically.

Step10: SBox and Box morphing

#1 shows the SBox node which changes each patch on the subdivided sur- face into a box. The depth of the box is also parametric and can be changed.

#2 shows the basic pattern which is inclosed by a bounding box.

#3 is the application of the Morph node, where the pattern in #2 is applied and morphed to the surface adjusting itself to fit in every patch.

Step10: rotation parameter

From the study of the fractals on the dome, it is evident that these panels are rotated at each layer to create greater complexity. Thus in #1 the rotate node was added to the definition to provide the ability of parametrically rotating each layer when needed.

#2 shows the juxtaposition of all the outer layers of the dome where the pat- tern is lost.

Step11: all in all

The following image shows the full definition and the outcome.

Step12: the Louvre as a rendering